Nash Equilibrium
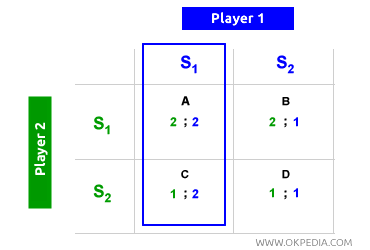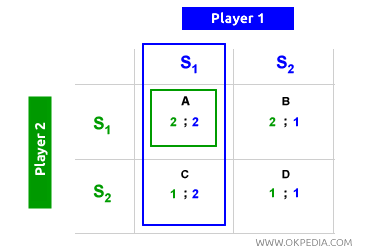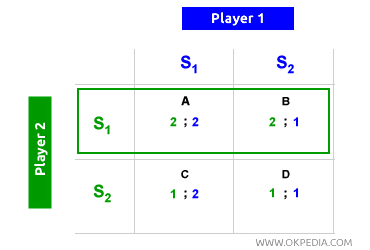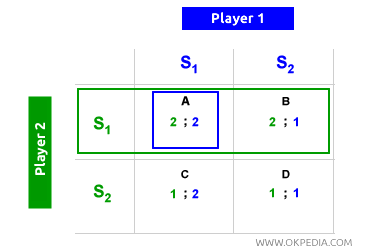
The Nash equilibrium is a situation where each player selects the best possible strategy (dominant strategy) based on their expectations of the other player's move. It represents the set of moves (m1, m2) where each player’s choice is the best response to the other’s action. Players form assumptions about each other’s choices and decide their own strategy accordingly (“doing what’s best for themselves and for others”). A Nash equilibrium is stable, as no player has an incentive to change their decision (strategy). Each player maximizes their own outcome, taking into account the best choice of the other. Any deviation would only worsen their position (payoff / utility). The Nash equilibrium is an optimal state in a non-cooperative game and is therefore also called a non-cooperative equilibrium. It doesn’t result from any agreement between players; instead, it emerges as each player adopts dominant strategies that ensure the best individual outcome and the best collective balance. The following payoff matrix illustrates a Nash equilibrium in a two-player non-cooperative game. While this example involves two players, the concept can extend to N players.
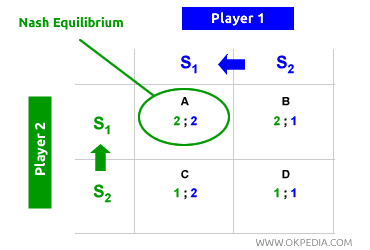
In the matrix, each player can choose either strategy S1 or S2. Player S1 expects player 2 to choose S1 (their dominant strategy) and, therefore, also opts for S1 since it offers an individual payoff of 2. Similarly, player 2 anticipates player 1’s choice of S1 and selects S1 as well. The equilibrium of the game thus converges to cell A in the matrix (top left), where both players maximize their individual payoffs (individual optimum) by choosing their dominant strategies (Nash equilibrium). Both players hypothesize the optimal move (dominant strategy) of their opponent and, based on that, choose their dominant strategies. The following example helps clarify the decision-making process behind the Nash equilibrium.
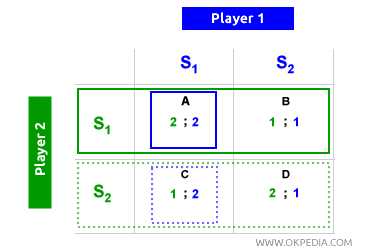
Player 1 (green) can choose either S1 or S2, and in both scenarios, they aim to achieve the highest payoff (2) found in cells A and D. However, player 1 knows that if they pick S2, player 2 (blue) would respond with S1, and the equilibrium would settle in cell C, where player 1’s payoff is the lowest (1). By choosing S1, player 1 knows that player 2 would also find it optimal to choose S1, leading to an equilibrium in cell A where the payoff is highest (2). Following the same logic, when it’s player 2’s turn to choose first, they recognize that selecting S1 would prompt player 1 to also choose S1, establishing the equilibrium again in cell A. Cell A is the Nash equilibrium, while the other cells are not. In summary, the Nash equilibrium is often described as: “Winning by doing what’s best for oneself and others.” It’s a fundamental concept in game theory and political economy.
Social Optimum. In a Nash equilibrium, it’s possible to have an optimal outcome for both players and society as a whole. For example, when player 1 (green) chooses S1 first, player 2 (blue) follows with S1, leading to an equilibrium in cell A. When player 2 (blue) chooses S1 first, player 1 (green) also picks S1, resulting again in cell A. Thus, cell A is a Nash equilibrium. Here, both players receive a payoff of 2 (individual optimum), and the combined payoffs (2+2) total 4 (social optimum). Therefore, in cell A (Nash equilibrium), there is both an individual and social optimum.
Multiple Nash Equilibria. A non-cooperative game may have several Nash equilibria. Even when multiple equilibria exist, each Nash equilibrium remains stable, as any deviation would worsen the outcome for each player. For example, the following payoff matrix shows two symmetric Nash equilibria.
Absence of Nash Equilibrium. Another issue with the Nash equilibrium is that it may not always be present. Many games lack a Nash equilibrium. In the example below, no Nash equilibrium exists. When player 1 chooses S2, player 2 chooses S2, placing the equilibrium in cell D. Conversely, when player 2 chooses S2, player 1 picks S1, and the equilibrium falls in cell B. Therefore, there is no Nash equilibrium in this game.
Prisoner’s Dilemma. Adopting dominant strategies doesn’t always lead to a socially optimal equilibrium. Without sufficient information, a non-cooperative game might converge to a stable but suboptimal equilibrium. This is illustrated in the “prisoner’s dilemma,” where two players, even when making rational assumptions about their opponent’s behavior and choosing dominant strategies, end up in a suboptimal equilibrium (D) both individually and socially. Equilibrium D is a Nash equilibrium but not a Pareto optimum. In conclusion, the Nash equilibrium and Pareto optimum are distinct, as they arise from different conditions.
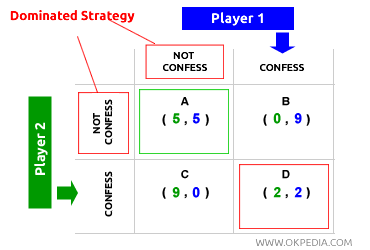
For instance, player 1 expects player 2 to confess, as confessing is player 2’s dominant strategy. By confessing, player 2 secures freedom (payoff 9). Based on this expectation, player 1 chooses the dominant option between B and D, deciding to confess as well to ensure a payoff of at least 2. Player 2 applies the same logic but in reverse. Equilibrium D is a Nash equilibrium and remains stable since neither player has an incentive to change their decision. However, equilibrium D is not a Pareto optimum, as both players receive a suboptimal payoff (2) compared to the higher payoff (5) they would receive if they both chose not to confess (equilibrium A).
Cournot Equilibrium. The Nash equilibrium is a theoretical balance concept similar to the Cournot equilibrium. In the Cournot duopoly, each firm selects the optimal level of production based on the strategic decision of the competing firm.
