Random Variable

A random variable represents the possible outcomes of a random phenomenon and can take on different values within a certain range. It is also known as a stochastic variable or simply a random variable (commonly abbreviated as r.v.).

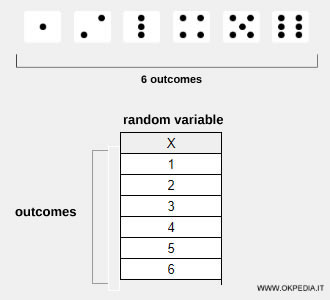
Example. The random variable X describes the outcomes {1, 2, 3, 4, 5, 6} from rolling a fair die. While we can’t predict which face will appear, we know it will be one of the six possible outcomes of X.

In probability theory, a random variable is the mathematical representation of the result of an uncertain, non-deterministic process.

Definition of a Random Variable

The formal definition of a random (or stochastic) variable is as follows:

Given a sample space {Ω} consisting of all n-tuple combinations of a statistical variable K, and a probability measure P defined on it, a random variable X is a measurable function from the sample space {Ω} to a target space E.

Each element in the sample space {Ω} maps to a single value that X may assume in the space E.

This definition extends the one originally proposed by Lindgreen.

Lindgreen’s Definition. A function X defined on the sample space {Ω} is said to be measurable with respect to the Borel σ-algebra β if and only if the set {ω ∈ Ω : X(ω) ≤ λ} belongs to β for every real number λ.

Types of Random Variables

Depending on the nature of the phenomenon being modeled, a random variable can be classified as:

• Discrete Random Variable
  If it takes values from a finite or countable set.
• Continuous Random Variable
  If it can take any value within the continuum of real numbers ℝ.

Probability Distribution

The probability distribution of a random variable X is a function that assigns to each possible value of X its associated probability P(X).

Practical Example

The random variable X represents the possible outcomes of a fair six-sided die.

Each face has an equal probability P(X) of 1/6, which corresponds to 0.17 or 17%.

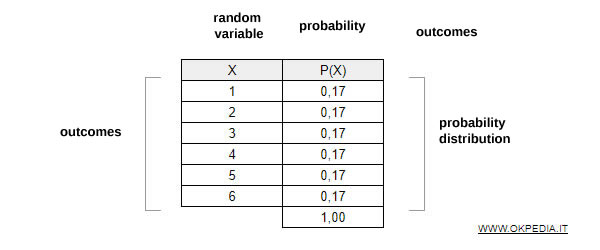
By assigning a probability to each possible outcome, we obtain the probability distribution of the random variable.

The sum of all probabilities in the distribution is always equal to 1.

Univariate and Multivariate Random Variables

Random variables can be classified based on dimensionality:

• Univariate Random Variables refer to single-dimensional random variables.
• Multivariate Random Variables (also called n-dimensional random variables) involve two or more dimensions.

Stochastic Processes

A stochastic process is a random variable whose value evolves over time (t), where time serves as the independent variable.