Least Upper Bounds in Sets
The least upper bound of a non-empty set A is defined as the smallest real number that is not less than any element within A.
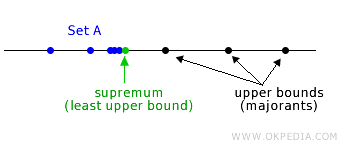
This concept is also referred to as the supremum of A.
The number, which may or may not be a part of A itself, effectively sets an upper limit for A and is represented by the symbol sup(A).
$$ \sup(A) $$
Detailed Look at Least Upper Bound
To get formal, for any non-empty set A consisting of real numbers, a number x qualifies as the supremum of A if:
- It acts as an upper bound for A, implying that x is either greater than or equal to every element in A $$ \forall \ a \in A \Rightarrow a \leq x $$
- It is the least of all such upper bounds, indicating that no other upper bound y of A is smaller than x $$ \forall \ y \in R \ , \ (\forall \ a \ \in A, a \leq y) \Rightarrow \sup(A) \leq y $$
When A's least upper bound is also among its elements, it's termed the maximum of A, noted as max(A). $$ \sup(A) \in A \Rightarrow \sup (A) = \max(A) $$
Illustrative Examples
Example 1
Consider the finite set A, where every element is no greater than 5, thus 5 serves as an upper bound (majorant) for A.
$$ A = \{1, 2, 3, 4\} $$
Yet, 4 stands out as the lowest of these upper bounds, making it the supremum of A.
$$ \sup(A) = 4 $$
Here, the supremum is also A's maximum.
$$ \sup(A) = \max(A) = 4 $$
Example 2
The set of natural numbers, being unbounded above, presents a unique case,
$$ N = \{1, 2, 3, 4, 5, \ldots \} $$
Its least upper bound stretches to positive infinity (∞), since no real number surpasses every natural number.
$$ \sup(N) = +\infty $$
In such a scenario, the least upper bound lies outside the set N, indicating that N possesses an least upper bound but lacks a maximum.
