Subset

Given two sets, A and B, we say that set A is a subset of set B if every element in A is also in B.

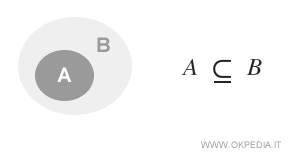
In this case, set A is entirely contained within set B.

In mathematical notation, this is written as A ⊆ B and read as "set A is a subset of B" or "set A is included in B".

Practical Example

A subset can be visually represented as follows:

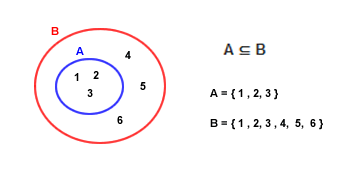
In the diagram, we have two sets, A and B.

• Set A contains the elements { 1, 2, 3 }.
• Set B contains the elements { 1, 2, 3, 4, 5, 6 }.

As you can easily see, set A is contained within set B. In other words, set A is a subset of B.

Normal vs. Strict Inclusion

The subset relationship can be normal or strict.

• Normal Inclusion (A⊆B)
  In normal inclusion, the sets can be equal (A=B). The two sets might even be identical.
  
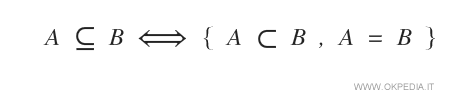
  A subset with a normal inclusion relationship is called:
  • a proper subset if the two sets are different (A≠B)
  • an improper subset if the two sets are the same (A=B) or if the subset is empty (A=∅).
  
  Practical Example
  
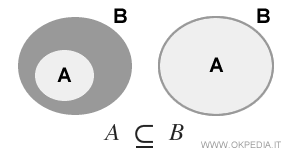
• Strict Inclusion (A⊂B)
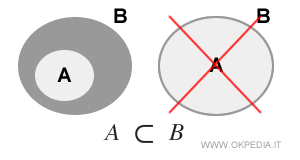
  In strict inclusion, the sets cannot be equal. The two sets are different (A≠B). Therefore, there are elements in set B that are not in set A. In such cases, we say that "set A is strictly included in B" or "set A is strictly contained in B", and it is denoted as A ⊂ B.
  
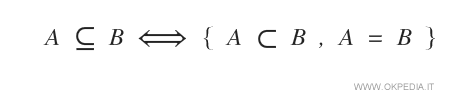
  A non-empty subset with a strict inclusion relationship is always a proper subset because the two sets are different.
  
  Practical Example
  
  

  Note. Strict inclusion (A⊂B) is always also normal inclusion (A⊆B). However, normal inclusion (A⊆B) is not necessarily strict inclusion (A⊂B) because the two sets might be identical.