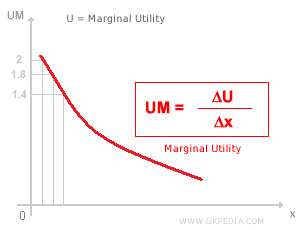
Marginal Utility
Marginal utility is the additional satisfaction or benefit a consumer gains from consuming one more unit of a good. Under the classical (cardinal) utility framework developed in the 19th century, it’s assumed that utility can be measured. According to this view, each additional unit consumed yields a smaller increase in total utility than the previous one. Graphically, the marginal utility function is represented as a downward-sloping curve, reflecting the principle of diminishing marginal returns. Note that the vertical axis in this graph represents marginal utility - that is, the incremental gain in utility from additional consumption - not total utility.
To further illustrate the concept, consider the following depiction of a utility function that shows the consumer’s total utility. Total utility, denoted as U, depends on the quantity of good X consumed. As consumption of good X (the independent variable) increases, the consumer’s total utility (the dependent variable) also rises.
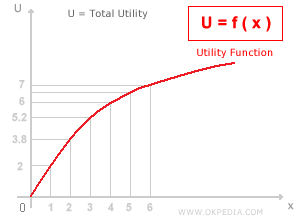
The total utility function is monotonically increasing. This means that if X > X*, then f(X) > f(X*), and therefore U(X) > U(X*). In consumer terms, increasing the quantity of good X leads to an increase in total utility U.
The second derivative of the total utility function is negative, indicating that the rate at which utility increases (i.e., marginal utility) declines as consumption rises - a reflection of diminishing marginal utility.
From a mathematical perspective, this declining marginal utility corresponds to the second derivative of the utility function, f″(x). This derivative captures how much additional utility changes as consumption increases.
MU = f″(x), f″(x) < 0
Up to this point, we’ve considered marginal utility in a basket containing a single good, X. The same principle can be extended to a basket containing multiple goods. For instance, given two goods, X1 and X2, the marginal utility of increasing consumption of good x1 is expressed as follows:
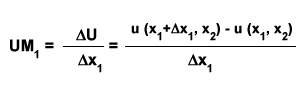
The principle of diminishing marginal utility underlies the convex shape of the indifference curve. The logic is simple: if the marginal gain from consuming more of one good decreases, then a balanced consumption of both goods yields greater total utility than concentrating consumption on just one.
Example. Imagine you’re extremely thirsty. You turn on the tap and pour yourself a glass of water. The first glass offers the greatest satisfaction because it quenches your thirst. In the graph above, the first unit on the x-axis (one glass) corresponds to a total utility of 2 on the y-axis. A second glass still increases your total utility, but to a lesser extent - say, to 3.8. This means the marginal utility of the first glass is 2, while the second adds just 1.8. And so on. As consumption increases, each additional unit provides less and less added satisfaction - the essence of diminishing marginal utility.
Marginal Utility and Economic Value. Marginal utility plays a key role in determining the economic value of a good. The greater the marginal utility, the higher the value or price a consumer is willing to pay. This relationship is rooted in the scarcity of the good relative to the consumer’s need. When a good is scarce in relation to demand, the marginal utility of each additional unit is high - and so is the market price. For example, someone who is very thirsty may be willing to pay a premium for a glass of water (high marginal utility). But as their need is satisfied, they’ll be less willing to pay as much for additional glasses, since the marginal utility of each successive unit declines.
