Indifference Curve

An indifference curve is a graphical representation that shows different combinations of consumption choices providing the same level of satisfaction to a consumer. Given two goods, x and y, the quantities of these goods that yield the same utility, U = U(q_x, q_y), are plotted as coordinates (x, y) on a graph. Connecting these points forms a curve, where the utility level remains constant.

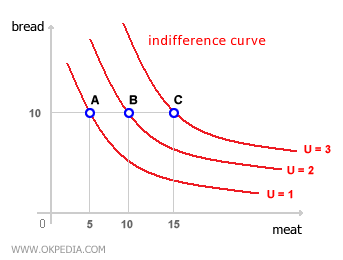
For example, in the following indifference curve, we place "bread" on the y-axis and "meat" on the x-axis. Points A and B represent two different bundles of the two goods, and both give the same level of utility, U_A=U_B. Since these points deliver the same satisfaction to the consumer, they are "indifferent" when choosing between the two bundles. This is why it's called an indifference curve.

Following this logic, we can plot multiple indifference curves on the graph, each corresponding to a different utility level. The further the curve is from the origin, the higher the utility, as it represents the consumption of larger quantities of both goods. In the diagram below, for instance, the outer indifference curve is linked to bundle C (15, 10), which consists of 10 units of bread and 15 units of meat. Bundle C provides more consumption than both bundle A (5, 10) and bundle B (10, 10). According to the non-satiation assumption, the consumer always prefers the outer indifference curve because it offers a higher utility level.

The key characteristics of an indifference curve are as follows:

• Negative slope. An indifference curve slopes downward because, to maintain the same utility level, an increase in the consumption of one good must be offset by a decrease in the other (indifference curve slope).
• Convexity. Based on the principle of diminishing marginal utility, bundles that contain balanced quantities of both goods generally provide higher utility than those with extreme quantities of one good. For example, the bundle (10, 10) offers more utility than either (5, 15) or (15, 5). This characteristic is known as the convexity assumption of indifference curves.

Indifference curves never intersect because they represent different utility levels. If two indifference curves were to intersect, it would violate the basic assumptions of consumer preferences.

Marginal Rate of Substitution. Along an indifference curve, the trade-off between reducing the quantity of one good (-Δx1) and increasing the quantity of another (+Δx2) is known as the marginal rate of substitution (MRS) between the two goods. The MRS measures how much of one good the consumer is willing to give up in exchange for more of the other.

MRS = -Δx₁/Δx₂

The marginal rate of substitution is always negative because the indifference curve slopes downward. Since it is negative by definition, the MRS is often expressed as an absolute value.

|MRS| = |-Δx₁/Δx₂| = Δx₁/Δx₂

Since all points on an indifference curve correspond to the same utility level (U), the gain in utility from increasing the quantity of good x₂ exactly offsets the loss of utility from reducing the quantity of good x₁.

-Δx₁ MU_x1 = Δx₂ MU_x2

Therefore, the marginal rate of substitution is equal to the inverse of the marginal utilities of the two goods.

-Δx₁/Δx₂ = MU_x2/MU_x1

The marginal rate of substitution is a point-specific measure, meaning that even though total utility (U) remains the same along the curve, the MRS varies at each point. Graphically, the MRS is represented by the slope of a line tangent to any point on the indifference curve, making it a measure of the curve’s steepness at that point.