Walras' Law

Walras' Law is an economic principle within general economic equilibrium theory, developed by the French economist Léon Walras in 1874 as part of his general market equilibrium theory (Walrasian equilibrium).

According to Walras' Law, given any price vector P (p₁,...,p_n) and n markets, the total sum of the excess demand (d-s) across all n markets is zero.

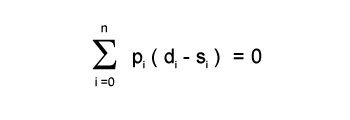
In the mathematical expression of Walras' Law above, the variable d_i represents the quantity demanded of good i, the variable s_i indicates the quantity supplied of good i, and p_i is the market price of good i.

Walras' Law asserts that the total value of excess demand p_i(d_i-s_i) for all n markets sums to zero.

Walras' Law is founded on the assumption that, in a perfectly competitive market, every economic agent operates under a balanced budget constraint of zero. For further information, refer to the proof of Walras' Law.

Corollary. An important corollary of Walras' Law states: given n markets, if n-1 markets are in equilibrium, then the nth market must also be in equilibrium. From a mathematical perspective, to satisfy Walras' Law, if n-1 markets are balanced (with zero excess demand) and the total excess demand across all n markets is zero, the nth market must also be in balance. For instance, if there are two markets and (d₁ - s₁) equals zero (market 1 is balanced), then (d₂ - s₂) must also be zero (market 2 is balanced). Otherwise, the equation p₁(d₁ - s₁) + p₂(d₂ - s₂) would not sum to zero.