Walrasian Equilibrium

Walrasian equilibrium refers to a market equilibrium under conditions of perfect competition. In an economy with N markets, a Walrasian equilibrium occurs when there is a price vector P( p₁, ... , p_n ) that balances supply S_n and demand D_n in each market.

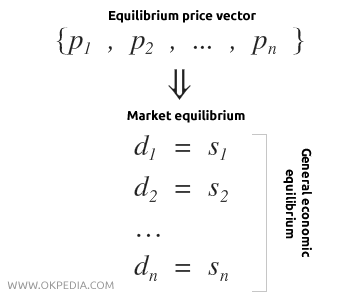
When all N markets are in equilibrium, it is referred to as general economic equilibrium (GEE). In this state, the excess demand (d_i-s_i) in each market is zero, meaning the sum of excesses across all markets is also zero.

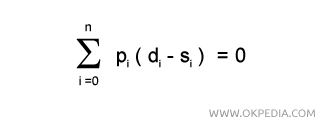
Each individual buys and sells exactly what they had planned.

Walrasian equilibrium also establishes the relative prices of goods, showing that the ratio between prices (relative prices) remains unchanged regardless of the good chosen as the numéraire.

Walras' Mathematical Model

To describe equilibrium, Léon Walras developed a mathematical model based on a system of two sets of equations.

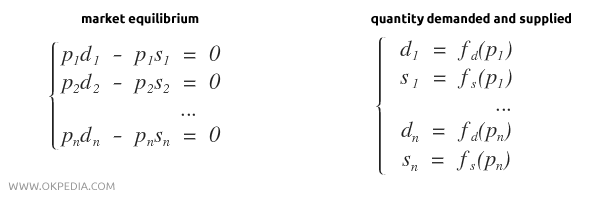
1. The first set of equations ensures that supply and demand are equal for each of the N goods (market equilibrium). There are as many markets as there are goods.
2. The second set expresses the quantity demanded (f_D) and quantity supplied (f_S) of each good as functions of its market price ( p_N ).

Prices and quantities demanded and supplied are interdependent variables. The price of a good determines its demand and supply, while demand and supply in turn affect its market price.

Walras’ model represents an ideal economy where individuals sell and buy exactly as they had planned.

The process of price formation in this model follows a trial-and-error approach known as tâtonnement.

Tâtonnement

The tâtonnement process is similar to collective bargaining seen in public stock auctions.

1. An auctioneer announces a price vector P( p₁, ... , p_n ). These are virtual prices, meaning no actual trades take place yet.
2. Based on this price vector, economic agents write down the quantity demanded D( d₁, ... , d_n ) and quantity supplied S( s₁, ... , s_n ) for each of the N goods on a ticket.

   Walras follows the methodological individualism of neoclassical economists. According to Walras, each individual makes decisions to maximize their own utility. Thus, the quantity of goods they demand or supply is what they believe best suits their own interests.

3. The auctioneer collects all the tickets and totals the quantities demanded and supplied for each good.
4. If demand equals supply ( d_i=s_i ) for every good, the auction concludes, the price vector becomes official, and actual trades are made based on the quantities listed on the tickets ( general economic equilibrium ).

   If there is any excess demand ( d_i≠s_i ), the auctioneer adjusts the prices in the markets that are not in balance, announces a new price vector, and the process starts again.

In general economic equilibrium, every individual achieves the best possible outcome based on market conditions, as they carry out their intended transactions.

In Walras' model, decisions are made individually, and trades are voluntary. There are no intermediaries or representative organizations (such as unions, lobby groups, or cartels). The market’s sole function is coordination.

As a result, if each individual maximizes their personal utility, the economic system as a whole reaches an optimal state in Walrasian equilibrium.

Pareto optimality. Walrasian equilibrium under perfect competition represents an efficient allocation in the Pareto sense (Pareto optimality). The link between competitive equilibrium and Pareto efficiency, in both consumption and production, is outlined in the first fundamental welfare theorem (welfare theorems).