Distance Between Two Vectors

Given two vectors in Euclidean space \( \mathbb{R}^n \): \[\vec{x} = (x_1, x_2, \ldots, x_n) \] \[ \vec{y} = (y_1, y_2, \ldots, y_n) \] The Euclidean distance between \( x \) and \( y \) is defined as the square root of the sum of the squared differences between their corresponding components: \[ \text{dist}(\vec{x}, \vec{y}) = \| \vec{x} - \vec{y} \| \] \[ = \sqrt{(x_1 - y_1)^2 + \ldots + (x_n - y_n)^2} \]

Geometrically, this distance corresponds to the length of the line segment connecting the two vectors in space.

It’s a straightforward generalization of the Pythagorean theorem to \( n \) dimensions.

Example

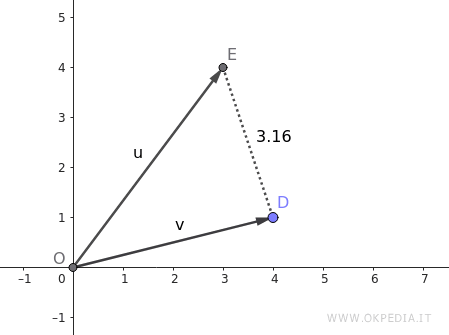
Let’s take the following vectors:

\[ \vec{u} = (3, 4) \]

\[ \vec{v} = (4, 1) \]

The distance between these vectors is approximately 3.16:

\[ \text{dist}( \vec{u}, \vec{v} ) = \sqrt{(3 - 4)^2 + (4 - 1)^2} = \sqrt{1 + 9} = \sqrt{10} \approx 3.16 \]

This means that vector \( \vec{u} \) lies about 3.16 units away from vector \( \vec{v} \) in the plane.

Properties of Euclidean Distance

The Euclidean distance satisfies the following fundamental properties:

• Symmetry
  The distance between two vectors is the same regardless of the direction of measurement. That is, going from \( x \) to \( y \) is equivalent to going from \( y \) to \( x \): \[ \text{dist}(x, y) = \text{dist}(y, x) \]
• Non-negativity
  The distance is always greater than or equal to zero, and it equals zero only when the two vectors are identical: \[ \text{dist}(x, y) \geq 0 \quad \text{and} \quad \text{dist}(x, y) = 0 \iff x = y \]
• Triangle Inequality
  This expresses the intuitive idea that the direct distance between two points is always less than or equal to any indirect route that passes through a third point. In other words, the straight path is the shortest: \[ \text{dist}(x, z) \leq \text{dist}(x, y) + \text{dist}(y, z) \]

These properties make the Euclidean distance a metric - a function that rigorously quantifies how far apart two points are in a geometric space.