Vector Norm
The norm of a vector - also known as its magnitude or length - is a function that assigns a non-negative real number to a vector, representing its length in the space \(\mathbb{R}^n\). For instance, given a vector \( x = (x_1, x_2, \ldots, x_n) \), its Euclidean norm is defined as: \[ \|x\| = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2} \]
The Euclidean norm extends the Pythagorean theorem to n-dimensional space.
Geometrically, the norm represents the vector’s distance from the origin. If the vector \( x \) starts at the origin \( O \), then \( \|x\| \) is the distance from \( O \) to the tip of the vector.
Example
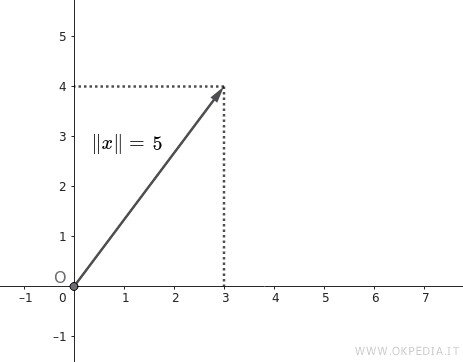
In \(\mathbb{R}^2\), consider the vector \( x = (3, 4) \).
The Euclidean norm of the vector is:
\[ \|x\| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
This represents the distance between the point (3, 4) and the origin (0, 0) in the Cartesian plane.
Other types of norms. While the Euclidean norm is the most commonly used, other norms are also important in various contexts. Examples include:
- \( \ell^1 \) norm (also known as the "Manhattan norm"): \[ \|x\|_1 = |x_1| + |x_2| + \cdots + |x_n| \]
- \( \ell^\infty \) norm (also known as the "maximum norm"): \[ \|x\|_\infty = \max \{ |x_1|, |x_2|, \ldots, |x_n| \} \]
Connection to the Dot Product
The norm of a vector can also be expressed in terms of the dot product, as follows:
\[ \|x\| = \sqrt{\langle x, x \rangle} \]
In other words, to compute the length of a vector \( x \), take the dot product of the vector with itself and then take the square root of the result.
Let’s consider a vector in \( \mathbb{R}^n \):
\[ x = (x_1, x_2, \ldots, x_n) \]
The dot product of \( x \) with itself is:
\[ \langle x, x \rangle = x_1 \cdot x_1 + x_2 \cdot x_2 + \ldots + x_n \cdot x_n = x_1^2 + x_2^2 + \cdots + x_n^2 \]
This is precisely the sum of the squares of the vector’s components - the expression found under the square root in the classical definition of the norm:
\[ \|x\| = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2} \]
So we can express it equivalently as:
\[ \|x\| = \sqrt{\langle x, x \rangle} \]
Properties of the Norm
The norm satisfies the following key properties:
- Non-negativity
The norm is always greater than or equal to zero, and equals zero if and only if the vector is the zero vector. \[ \|x\| \geq 0 \quad \text{and} \quad \|x\| = 0 \iff x = 0 \] - Homogeneity (scaling by a scalar)
Scaling a vector by a scalar scales its norm by the absolute value of that scalar. \[ \|\lambda x\| = |\lambda| \cdot \|x\| \] - Triangle inequality
The norm of the sum of two vectors is less than or equal to the sum of their norms - reflecting the idea that “the shortest path between two points is a straight line.” \[ \|x + y\| \leq \|x\| + \|y\| \]
