Dot Product of Vectors

Given two vectors \( x = (x_1, x_2, \ldots, x_n) \) and \( y = (y_1, y_2, \ldots, y_n) \) in \( \mathbb{R}^n \), the dot product, also known as the inner product, is defined as: \[ \langle x, y \rangle = \sum_{i=1}^n x_i y_i \] In other words: \[ \langle x, y \rangle = x_1 y_1 + x_2 y_2 + \ldots + x_n y_n \]

This operation yields a real number - a scalar - rather than a vector.

Geometrically, the dot product can also be interpreted in terms of the angle between the two vectors:

\[ \langle x, y \rangle = \|x\| \cdot \|y\| \cdot \cos\theta \]

Here, \( \|x\| \) and \( \|y\| \) denote the magnitudes (or norms) of the vectors, and \( \theta \) is the angle between them, ranging from 0° to 180°.

The dot product is especially useful for determining the angle between vectors and for checking orthogonality: \( \langle x, y \rangle = 0 \Rightarrow x \perp y \)

Key Properties of the Dot Product

The dot product satisfies several fundamental properties:

• Commutativity
  The order of the vectors does not affect the result: \[ \langle x, y \rangle = \langle y, x \rangle \]
• Linearity
  The dot product is linear with respect to vector addition and scalar multiplication, which makes it especially useful for analyzing linear combinations: \[ \langle ax + bz, y \rangle = a\langle x, y \rangle + b\langle z, y \rangle \quad \text{for all } a, b \in \mathbb{R} \]
• Positive-Definiteness
  The dot product of a vector with itself is always non-negative, and it equals zero if and only if the vector is the zero vector. This property underlies the definition of vector length (or norm): \[ \langle x, x \rangle = \|x\|^2 \geq 0 \quad \text{and } \langle x, x \rangle = 0 \iff x = 0 \]

Worked Example

Let’s go through a concrete example to compute the dot product of two vectors, determine their norms, and calculate the angle between them.

Consider the two vectors in the plane:

\[ x = (2, 3), \quad y = (4, -1) \]

We start by applying the definition of the dot product:

\[ \langle x, y \rangle = x_1 y_1 + x_2 y_2 \]

Substituting the components:

\[ \langle x, y \rangle = 2 \cdot 4 + 3 \cdot (-1) = 8 - 3 = 5 \]

So the dot product of \( x \) and \( y \) is 5.

Next, let’s compute the angle between the vectors.

We use the geometric form of the dot product to solve for the cosine of the angle:

\[ \langle x, y \rangle = \|x\| \cdot \|y\| \cdot \cos\theta \]

Solving for \( \cos\theta \):

\[ \cos\theta = \frac{\langle x, y \rangle}{\|x\| \cdot \|y\|} = \frac{5}{\sqrt{13} \cdot \sqrt{17}} \]

The norm (or magnitude) of a vector is calculated as:

\[ \|x\| = \sqrt{x_1^2 + x_2^2} = \sqrt{2^2 + 3^2} = \sqrt{13} \]

Similarly, for \( y \):

\[ \|y\| = \sqrt{y_1^2 + y_2^2} = \sqrt{4^2 + (-1)^2} = \sqrt{16 + 1} = \sqrt{17} \]

Now we substitute these values back into the formula:

\[ \cos\theta = \frac{5}{\sqrt{13} \cdot \sqrt{17}} \]

Since \( \cos\theta > 0 \), the angle between the vectors is acute (less than 90°).

Let’s estimate the square roots: \( \sqrt{13} \approx 3.6056 \), \( \sqrt{17} \approx 4.1231 \)

\[ \cos\theta \approx \frac{5}{3.6056 \cdot 4.1231} = \frac{5}{14.867} \approx 0.3362 \]

Now we compute the arccosine to find the angle whose cosine is 0.3362:

\[ \theta \approx \arccos(0.3362) \approx 70.35^\circ \]

So the angle between the two vectors is approximately \( \theta \approx 70.35^\circ \)

Since this value lies between 45° and 90°, the angle is acute but not particularly narrow.

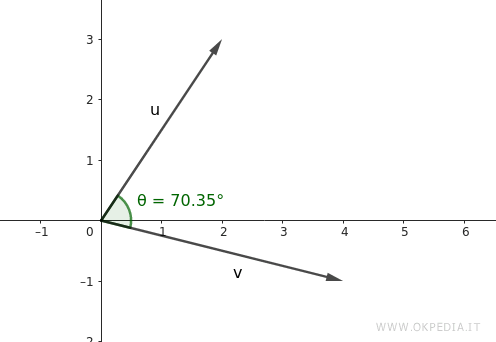
This example clearly illustrates the connection between the algebraic and geometric perspectives on the dot product.