Isoquant Curve

The isoquant curve is a graphical representation of an isoquant on a Cartesian plane. It maps out the quantities of two distinct production inputs along the axes, illustrating how a two-input production function operates. Each isoquant curve shows all the efficient combinations of these inputs that yield a specific level of output. In other words, every isoquant curve corresponds to one and only one output level.

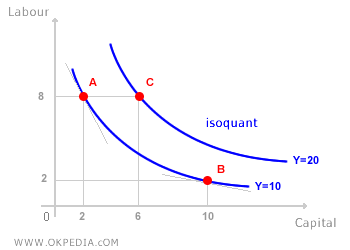
On the isoquant curve, point A represents a labour-intensive production method, utilizing 8 units of labor and 2 units of capital. Conversely, point B illustrates a capital-intensive approach, with 2 units of labor and 6 units of capital. Since both points lie on the same isoquant curve, they result in the same level of output (Y=10). Isoquant curves that lie further outward represent higher production levels, as they involve greater input usage. For instance, point C reflects a combination similar to B but with a higher capital input, which inevitably leads to increased output. The key characteristics of isoquant curves are as follows:

• Downward slope. An isoquant curve slopes downward because decreasing the quantity of one input necessitates increasing the other to maintain the same level of output (monotonicity).
• Convexity. Isoquant curves are convex due to diminishing marginal returns—meaning that as you increase the quantity of one input, progressively larger reductions in the other input are required to maintain output levels.
• Non-intersecting. Isoquant curves do not overlap, as each represents a unique level of production. If two isoquants were to intersect, it would create ambiguity regarding which curve corresponds to a higher output level.

Every point along an isoquant curve represents a distinct input ratio that achieves the same level of production. This ratio, known as the marginal rate of technical substitution, is given by the slope of the tangent line at that particular point on the curve.