Marginal Rate of Technical Substitution
The marginal rate of technical substitution (MRTS) measures how one input can be substituted for another while keeping output constant, given a fixed level of technology. It is commonly abbreviated as MRTS and is also referred to as the Marginal Rate of Technical Substitution. This metric indicates how much of input X1 must be increased when input X2 is reduced, and vice versa, to maintain the same level of production—essentially staying on the same isoquant curve. For a production function with two inputs, the marginal rate of technical substitution is expressed as follows:
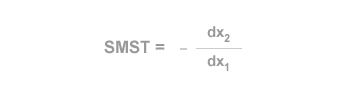
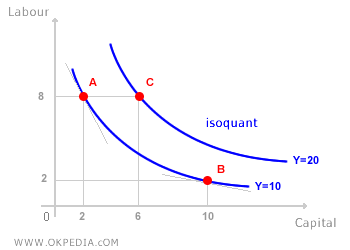
Graphically, the marginal rate of technical substitution corresponds to the slope of the isoquant—that is, the incline of the tangent line at a given point on the isoquant curve. Since isoquants slope downward, the MRTS is always negative. As illustrated in the diagram below, the slope of the isoquant changes at every point along the curve. For example, the tangent line at point A is steeper than the tangent at point B. As we’ll see in the next section, this variation is directly linked to the marginal productivity of inputs and the principle of diminishing marginal returns.
The marginal rate of technical substitution is equal to the inverse ratio of the marginal productivities of the two inputs. Under conditions of perfect competition, this ratio also equals the ratio of the inputs' prices. Below is the mathematical proof demonstrating the relationship between the marginal rate of technical substitution (MRTS) and the marginal productivity of inputs.
Measuring Units of Inputs. The value of the marginal rate of technical substitution depends on the unit of measurement chosen for each input. To obtain a more standardized measure, it is often preferable to use the elasticity of substitution.
