Risk Neutrality
Risk neutrality describes an individual's stance toward risk. A person is said to be risk neutral when the utility of the expected monetary value of a lottery is equal to the expected utility of its outcomes. In other words, given a lottery (a random variable) with two possible outcomes X1 and X2, and corresponding probabilities p1 and p2, risk neutrality can be expressed with the following equation:
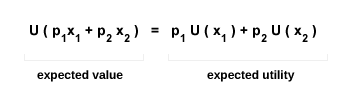
On the left-hand side, we have the utility of the expected value of the lottery. On the right-hand side, we have the expected utility itself. In this case, the individual is indifferent between receiving a guaranteed sum equal to the expected value and taking part in the lottery. This behavior can be visualized using the following Cartesian diagram:
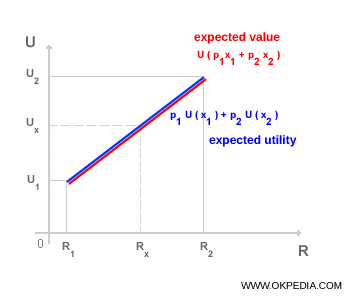
The diagram plots the utility of the expected value (in red) and the expected utility function (in blue). The two functions coincide, indicating that the individual has no preference between a certain outcome and a risky one with the same expected value. In essence, a risk-neutral person evaluates decisions purely based on expected monetary outcomes, without factoring in risk.
Corollary. An individual is risk neutral if the expected value of the lottery is equal to its certainty equivalent.
