Convexity Axiom
The convexity axiom states that consumers tend to prefer diversified bundles of goods over extreme ones. This behavior stems from the principle of diminishing marginal utility: the additional satisfaction gained from consuming more of the same good declines as its quantity increases. The axiom is named for the convex shape of consumer preference sets when plotted on a Cartesian plane - an implication that gives rise to the typical shape of the indifference curve. Given two equally preferred bundles, A and B, a consumer will favor a third bundle, C, which combines the two, as it yields a higher overall utility. Graphically, this preference for balanced consumption is illustrated through combinations of the two goods.
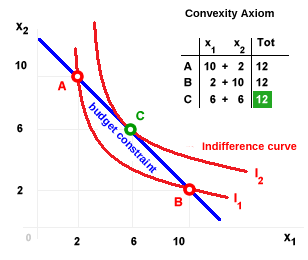
In the diagram, the budget constraint (the blue line) represents all feasible combinations of the two goods a consumer can afford. The red curves are indifference curves, each representing different levels of utility. Consider three bundles - A, B, and C - all lying on the same budget line and involving the same total quantity of goods (12 units). Despite this, the consumer does not view them as equally desirable. As consumption becomes increasingly skewed toward one good, the marginal benefit of consuming additional units of that good diminishes. As a result, the more balanced bundle C lies on a higher indifference curve (I2) than the more polarized bundles A and B, which both lie on a lower curve (I1). Since I2 lies farther from the origin, it corresponds to a higher level of total utility. We can summarize this as:
U(C) > U(A)
U(C) > U(B)
U(A) = U(B)
From the consumer’s standpoint, bundle C is therefore strictly preferred to both A and B, as it delivers a greater level of satisfaction. In short, intermediate combinations of goods typically result in higher values of the consumer's utility function than more extreme allocations.
