Transitivity Axiom

The transitivity axiom is a cornerstone of consumer preference theory, ensuring that a consumer's choices are logically consistent. It states that given three bundles - A, B, and C - if the consumer prefers A to B and B to C, then they must also prefer A to C. Graphically, this axiom implies that indifference curves cannot intersect; if they did, the internal logic of consumer preferences would break down. The diagram below illustrates a hypothetical case in which two indifference curves intersect, involving three consumption bundles.

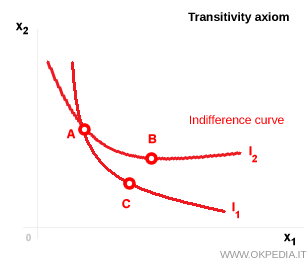
In this example, the indifference curves fail to reflect a consistent ranking of preferences. For instance, bundles A and B lie on the same indifference curve, $I_2$, meaning the consumer derives the same level of utility from both. The same is true for bundles A and C, which both lie on curve $I_1$. According to the transitivity axiom, this should imply indifference between B and C as well. However, that’s not the case - bundle B lies on a higher indifference curve than C, making it strictly preferable. This leads to a clear contradiction:

$$ B \succ C $$ $$ A = C $$ $$ A = B $$

If the consumer is indifferent between A and B, and also indifferent between A and C, then they cannot rationally prefer B to C. The transitivity axiom is precisely what prevents such contradictions in a coherent model of consumer behavior.