Indifference Curve Slope
The slope of an indifference curve reflects the marginal rate of substitution between two goods. For any two goods, X1 and X2, the indifference curve represents all the combinations of these goods (or consumption bundles) that provide the consumer with the same level of satisfaction. As the consumption of one good increases, the quantity of the other must decrease to maintain constant utility. This trade-off explains the downward slope of the curve. The slope can be computed as the absolute value of the ratio of the change in quantity of good x2 to the change in quantity of good x1 (see marginal rate of substitution), or as the first derivative of the indifference curve equation.
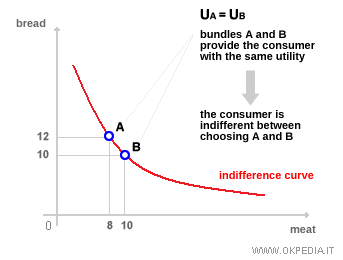
The slope varies along the indifference curve, giving it its characteristic curvature. This variation is driven by the principle of diminishing marginal utility: as consumption of one good increases, the additional utility gained from each extra unit tends to decline. As a result, the curve becomes flatter at the extremes - where one good is consumed in much larger quantities than the other - and more convex in the middle, where the goods are consumed in more balanced proportions (see convexity of indifference curves).
