Production Function

The production function describes the relationship between the quantity of a good produced (output) and the amounts of various production inputs. It is a fundamental concept in microeconomics used to analyze production choices. Mathematically, it expresses how the output (Y) of a good depends on the input (X) of multiple production factors over a given period.

Y = f ( x₁ , x₂, x₃, ... , x_n)

Given a production set Z, the production function determines the maximum possible output for a specific combination of productive inputs, assuming a fixed amount of capital over a set period. In the simplest case, where there is only one product (Y) and one input (X), the production function is expressed as:

Y_q = f ( x_q )

When dealing with a single product and a single input, the production function can be easily visualized on a Cartesian plane, with output (Y) on the vertical axis and the quantity of input (X) on the horizontal axis. The graphical representation of this function is known as the production curve.

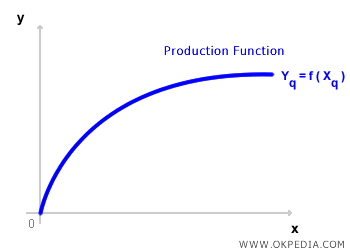
In graphical terms, the production function corresponds to the frontier of the production set. It represents the production process that maximizes output (Y) for each level of input (X). Mathematically, the production function has the following key properties:

• Continuity. The production function is continuous because both output (Y) and input (X) can be divided into infinitely small increments.
• Monotonicity. The function is monotonic, meaning that increasing the quantity of input (X) never leads to a decrease in output (Y).

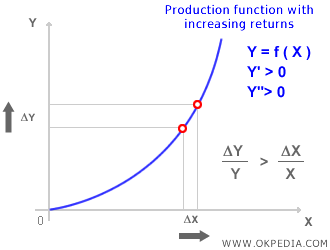
The shape of the production function depends on the returns to scale. It can exhibit decreasing, constant, or increasing returns. Returns to scale are:

• Constant: When output changes in direct proportion to the change in inputs.
• Increasing: When output grows at a faster rate than input usage.
• Decreasing: When output grows at a slower rate than input usage.

In cases of increasing returns to scale, the production function appears as follows:

Homogeneous Functions. A homogeneous function of degree k provides a straightforward way to represent different types of returns to scale. The degree of homogeneity (k) determines how the function behaves:

• k = 1: Constant returns to scale.
• k > 1: Increasing returns to scale.
• k < 1: Decreasing returns to scale.

Short-Run Production Function. In the short run, the production function shows the relationship between inputs and output under the assumption that capital and technology remain fixed. This means it represents a static production curve. The only way a firm can adjust production in the short run is by altering the quantity of variable inputs, such as labor. However, the firm cannot change its production capacity or upgrade technology. The available input combinations are fixed and constrained by the production frontier.

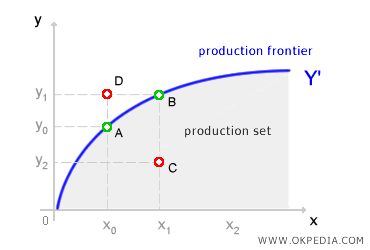
For example, in the graph above, points A and B lie on the production frontier and represent efficient input-output combinations since they maximize output (Y) for a given level of input (X). Point C is still within the production set and feasible, but it is inefficient because it results in a lower output (Y₂) compared to the maximum attainable (Y₁) for the same level of input (X₁). Meanwhile, point D is unattainable since it lies beyond the production frontier.

Technological Progress. In the long run, firms can expand production capacity and adopt new technologies, leading to improvements in productivity and efficiency. As technological advancements occur, the production function undergoes significant shifts. Graphically, assuming technological progress boosts output per unit of input, the production function shifts upward, resulting in a dynamic curve.

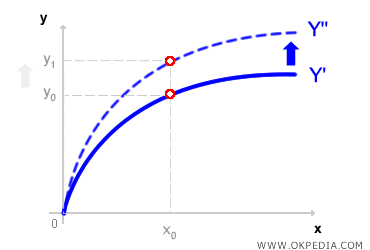
Technological innovations allow firms to produce more output with the same amount of inputs or reduce input usage while maintaining the same level of output, thereby increasing production efficiency.