General Equilibrium of Pure Exchange

The general equilibrium of pure exchange refers to a general economic equilibrium where goods are allocated in a Pareto-efficient manner (Pareto optimality). In a Pareto optimal outcome, no individual can enhance their well-being without diminishing someone else's. In a pure exchange economy with two economic goods (X, Y) and two consumers (A, B), this equilibrium can be illustrated using an Edgeworth box. The graphical representation of a general equilibrium of pure exchange is shown below:

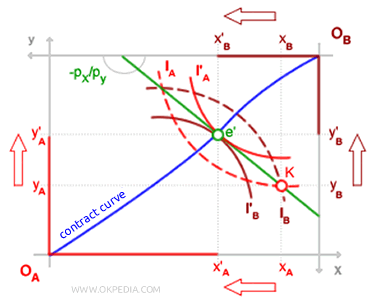
The indifference curves for consumer A are convex relative to origin O_A, while those for consumer B are convex relative to origin O_B. The axes measure the total available quantities of goods X and Y. For example, at the initial inefficient point K, consumer A holds an endowment of goods (x_A, y_A), while consumer B holds an endowment of (x_B, y_B). Point K is inefficient because both consumers could improve their well-being through trade. Consumer A might give up part of their endowment of good X, from x_A to x'_A, to increase their holding of good Y, from y_A to y'_A. This allows consumer A to reach a higher indifference curve I_A. Similarly, consumer B can give up some of their endowment of good Y, from y_B to y'_B, in exchange for more of good X, from x_B to x'_B, moving to a higher indifference curve I_B. This trading process enables both consumers to improve their well-being (a Pareto improvement). The reallocation continues until point e, where neither consumer can further improve their well-being without reducing that of the other (Pareto optimum). Geometrically, the Pareto optimum occurs where the indifference curves are tangent, meaning that the marginal rates of substitution for both consumers are equal.

MRS_A = MRS_B

The set of all points where the indifference curves are tangent (Pareto-efficient allocations) is called the contract curve. In a general equilibrium of pure exchange, the marginal rate of substitution matches the ratio of the goods' prices: the price of good X (p_x) and the price of good Y (p_y).

MRS = - p_x/p_y

From a geometric perspective, this means that at an efficient allocation point, the slope of the indifference curves (MRT) matches the slope of the budget constraint line. At this point (e'), the general equilibrium of pure exchange is Pareto-efficient. Given a fixed total endowment of goods (X and Y), each consumer (A, B) maximizes their well-being without diminishing the other's.