Welfare Theorems
The welfare theorems are foundational principles in political economy, linking Pareto-efficient allocations (Pareto optimality) to Walrasian competitive equilibrium (Walrasian equilibrium). These theorems rest on the belief in the superiority of a competitive free market, a perspective developed by neoclassical economists to highlight the inefficiencies of state intervention and central planning in economic systems. The main welfare theorems are as follows:
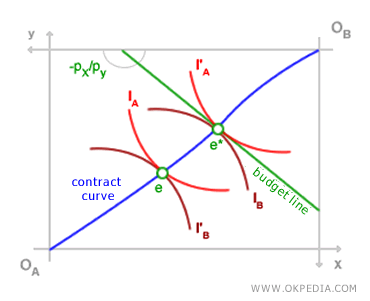
- First Welfare Theorem. The first welfare theorem states: "a Walrasian competitive equilibrium is Pareto efficient" (Pareto efficiency). This occurs when, at the optimal point, the ratio of marginal rates of substitution MRSA/MRSB equals the slope of the budget constraint -px/py. At point e*, both a competitive equilibrium (Walrasian equilibrium) and a Pareto optimal outcome (Pareto efficiency) are achieved. The allocation of resources in a perfectly competitive market is Pareto-efficient.
- Second Welfare Theorem. The second welfare theorem states: "for any Pareto-optimal allocation, there exists a set of allocations that correspond to a Walrasian competitive equilibrium". For example, given the relative prices of goods X and Y, two consumers, A and B, may start at point K (non-optimal). Consumer A’s initial endowment is (xA, yA), while consumer B’s is (xB, yB). Even though point K lies on the budget line, it is not Pareto optimal because both consumers can improve their welfare through trade, eventually reaching point e', where they both attain a higher indifference curve (a more favorable outcome). At point e', both a competitive equilibrium (Walrasian equilibrium) and a Pareto optimal outcome (Pareto efficiency) are realized.
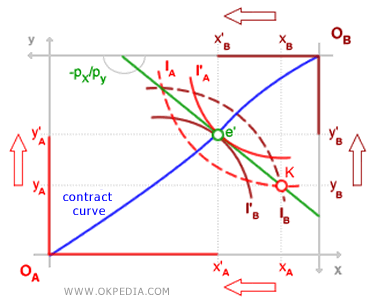
The second welfare theorem applies to both exchange and production. If indifference curves are convex, and isoquant curves are also convex, there exists a price vector and a distribution of resources for every Pareto-efficient allocation that ensures both Walrasian equilibrium and efficient allocation (Pareto optimality).
The first welfare theorem establishes the relationship between Pareto-efficient allocations and competitive equilibrium (Walrasian equilibrium). The second welfare theorem reverses this, showing that any competitive equilibrium (Walrasian equilibrium) corresponds to a Pareto-efficient allocation.
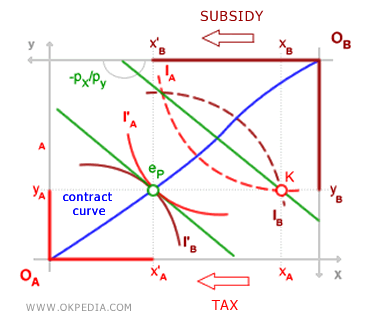
Market and Planning. The second welfare theorem also demonstrates that the allocation achieved through market equilibrium is equivalent to that reached by a central planner or policy maker. By adjusting initial endowments using redistributive tools like taxes and subsidies, it is possible to achieve any Pareto-efficient social state along the contract curve. For example, starting from a non-optimal point K, a central authority might tax consumer A’s endowment of good X and transfer it as a subsidy to consumer B, moving the system to an optimal (Pareto optimal) and equilibrium point eP. Such redistributive policies would still allow for a socially optimal, Pareto-efficient equilibrium.
However, no policy maker or central planner can possess all the information needed to implement redistribution effectively. Even assuming a benevolent central authority (acting in good faith) could reach a Pareto-optimal equilibrium through redistributive policies, the decentralized approach of the market remains simpler and less costly. Thus, relying on a perfectly competitive market is a more efficient, decentralized method for achieving Pareto-optimal equilibrium without the need for excessive information, coordination costs, or interventions.
Equity and Efficiency. The second welfare theorem distinguishes between equity (fairness) and efficiency. It acknowledges that a central authority (planner or policy maker) can intervene to modify initial allocations to make the system more equitable without compromising allocative efficiency. For instance, equilibrium eP might be socially preferable to market equilibrium e'. This allows for equity to be achieved without sacrificing the Pareto-efficient allocation of resources.
