General Equilibrium in Production

The general equilibrium in production refers to a general economic equilibrium where the allocation of production factors achieves Pareto efficiency. Considering two products, A and B, and two factors of production, K (capital) and L (labor), the isoquant curves for both products can be illustrated within an Edgeworth box. The lengths of the axes represent the total quantity of each production factor available in the economy, while the curves depict the isoquants for producing goods A and B. The graphical representation of a general equilibrium in production is shown below:

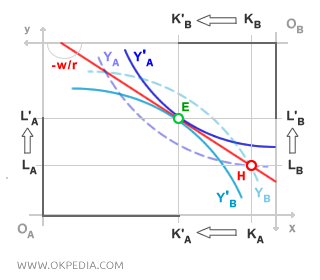
The isoquant curves Y_A (production of good A) are measured from origin O_A, while those for Y_B (production of good B) are measured from origin O_B. At the initial inefficient point (H), the production of good A utilizes K_A units of capital and L_A units of labor. Point H lies on the isoquant curve Y_A. Simultaneously, at point H, the production of good B uses K_B units of capital and L_B units of labor, lying on the isoquant curve Y_B. This allocation of factors (H) between the two products is inefficient. Improving efficiency is possible by reallocating some capital from production A to production B, and some labor from production B to production A. This reallocation increases the total output of goods A and B using the same quantities of capital and labor (K, L). The process concludes at point E, where the economy reaches higher (more favorable) isoquant curves for both products.

Y'_A > Y_A
Y'_B > Y_B

Since no further improvements can be made in Pareto terms, point E represents a Pareto-efficient equilibrium (Pareto optimum). At this optimal equilibrium, the isoquant curves for both goods become tangent, indicating the equality of the marginal rate of technical substitution (MRTS) between the production of goods A and B.

MRTS_A = MRTS_B

The set of points where the isoquants are tangent (Pareto-efficient allocations) is known as the contract curve.

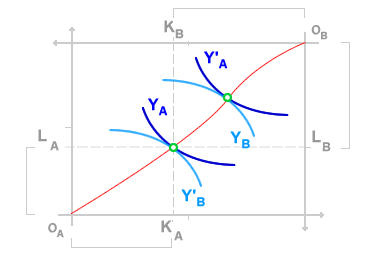
In a general economic equilibrium for production, the marginal rate of technical substitution (MRTS) matches the ratio of the prices of the production factors - wages (w) and interest (r).

MRTS = - w/r

From a geometric perspective, this means that at an efficient allocation point, the slope of the isoquants (MRTS) at the point of tangency equals the slope of the budget constraint line (- w/r). At point E, the general equilibrium in production is Pareto-efficient because, with the same use of production factors (K, L), the economy maximizes the output of both goods A and B.