Consumer Equilibrium

Consumer equilibrium refers to the combination of goods that enables a consumer to maximize their utility within a set budget. Given the consumer's preferences (indifference curves) and their income (represented by the budget line or budget constraint), and the prices of two goods, A and B, with prices P_A and P_B, equilibrium is reached where the budget line touches an indifference curve. This can be illustrated graphically on a Cartesian plane.

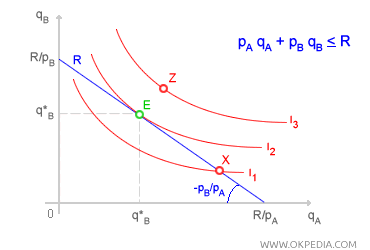
At the tangency point E, the slope of the indifference curve reflects the ratio of the marginal utilities of goods A and B (marginal rate of substitution), while the slope of the budget line represents the ratio of their prices, P_B/P_A.

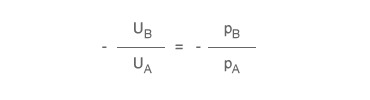
By applying a straightforward algebraic step, this equation can be transformed into the condition where the marginal utilities of the goods, weighted by their prices, are equal.

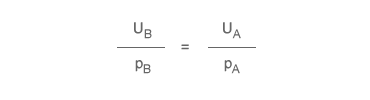
Consumer equilibrium represents an optimal choice, as any other affordable combination (those along the budget line) would lie on a lower indifference curve and thus provide less utility (e.g., point X). Conversely, points outside the budget line represent unattainable combinations, as they would require more spending than the consumer's available income R (e.g., point Z). Therefore, given income R and the relative prices P_A/P_B, at equilibrium point E, the consumer achieves the highest possible level of utility.